اگر نگاهی به پروتکل بیت‌کوین داشته باشید، اطلاعات خوبی در خصوص مبانی ریاضی ارزهای دیجیتال به دست خواهید آورد. یکی از دلایلی که باعث می‌شود تا بیت‌کوین برای تازه‌کارها گیج‌کننده باشد، این است که فناوری آن مفهوم مالکیت را به گونه‌ای دیگر تعریف کرده است. در رویکرد سنتی، در صورتی که شما مالک چیزی مانند یک خانه یا یک مقدار پول باشید، سرپرستی آن چیز را در اختیار دارید یا یا این‌که این سرپرستی را به یک موجودیت قابل اطمینان دیگر مانند یک بانک واگذار می‌کنید. در این مطلب سعی داریم تا در مورد اصول ریاضی بیت‌کوین صحبت کنیم. با ما همراه باشید.

پروتکل بیت‌کوین

پروتکل بیت‌کوین فرق دارد. بیت‌کوین به صورت متمرکز یا محلّی ذخیره نمی‌شود و بنابراین، هیچ کسی سرپرست آن نیست. بیت‌کوین‌ها به صورت یک سری رکورد در یک دفتر معین توزیع‌شده به نام بلاکچین ذخیره می‌شوند و یک نسخه از آن هم در یک شبکه‌ داوطلبانه ذخیره می‌شود که از یک تعداد رایانه متصل به یکدیگر تشکیل شده است. «مالکیت» بیت‌کوین به این معنا است که مالک می‌تواند با ایجاد یک رکورد انتقالی در بلاکچین به فرد دیگری واگذار کند. چه چیزی این قابلیت را اعطا می‌کند؟ دسترسی به یک جفت کلید خصوصی و عمومی ECDSA. این به چه معنا است و چگونه می‌تواند بیت‌کوین را امن سازد؟

بیایید زیر این چتر نگاهی به این موضوع داشته باشیم.

ECDSA مخفف کلمات الگوریتم امضای دیجیتال منحنی سهموی است. در این فرآیند از یک منحنی سهموی و یک میدان محدود برای «امضای» داده استفاده می‌شود، به طوری که اشخاص ثالث می‌توانند اصالت امضا را تأیید کنند. در عین حال، امضاکننده همچنان می‌تواند امضا را خلق کند. در بیت‌کوین، داده‌ای که امضا می‌شود، همان تراکنشی است که مالکیت طی آن انتقال پیدا می‌کند.

در ECDSA رویه‌های مجزایی برای امضا و تأیید وجود دارد. هر یک از این رویه‌ها در واقع یک الگوریتم است که از چند عملیات منطقی تشکیل شده است. در الگوریتم امضا از کلید خصوص استفاده می‌شود و در فرآیند تصدیق، از کلید عمومی بهره‌برداری می‌شود. در این خصوص، در ادامه مثالی را بیان خواهیم کرد.

اما اول، مقداری در خصوص منحنی‌های سهموی و میدان‌های محدود صحبت می‌کنیم.

منحنی‌های سهموی و پروتکل بیت‌کوین

منحنی سهموی از نظر جبری به صورت معادله‌ای به شکل زیر است:

y2 = x3 + ax + b

به ازای a = 0 و b = 7  یعنی آن چیزی که در بیت‌کوین از آن استفاده می‌شود، این منحنی به شکل زیر است:

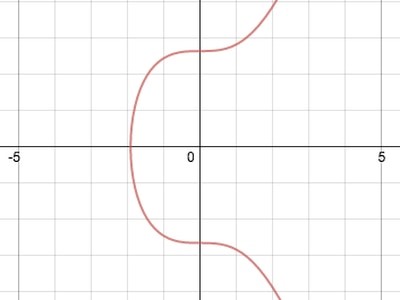
ریاضیات مربوط به بیت‌کوین

منحنی‌های سهموی دارای ویژگی‌های سودمندی هستند. مثلاً دو خط غیرعمودی که دو نقطه‌ غیرمماس را بر روی نمودار قطع می‌کنند، همیشه نقطه سومی را هم بر روی منحنی قطع می‌کنند. یک ویژگی دیگر هم آن است که یک خط غیر عمودی مماس بر منحنی در یک نقطه، دقیقاً یک نقطه دیگر بر روی منحنی را هم قطع می‌کند.

می‌توانیم از این ویژگی‌ها استفاده کرده و دو عملیات را تعریف کنیم: جمع نقطه و دو برابر کردن نقطه.

جمع نقطه: P + Q = R به صورت نقطه‌ای بر روی محور x از سومین نقطه تقاطع R’ بر روی خطی تعریف می‌شود که از P‌ و Q  هم عبور می‌کند. این مسأله را می‌توانید به سادگی در نمودار زیر مشاهده کنید:

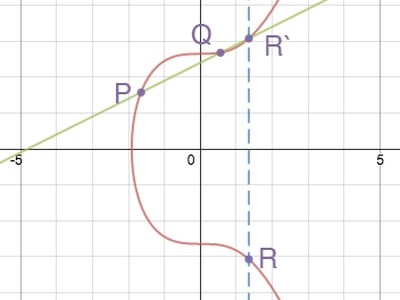
ریاضیات مربوط به بیت‌کوین

به همین ترتیب، دو برابر کردن نقطه، P + P = R  با پیدا کردن خط مماس بر نقطه‌ای که دو برابر می‌شود، یعنی P و همچنین، نقطه‌ای بر روی محور x که نقطه R’ بر روی منحنی قطع می‌کند تا R ‌حاصل شود، به دست می‌آید. در زیر نمونه‌ای از این را مشاهده می‌کنید.

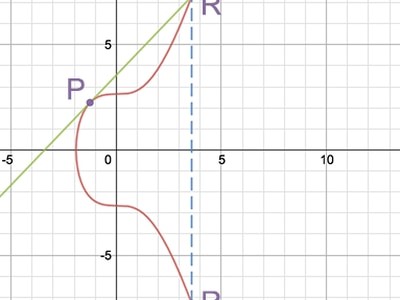
دو برابر شدن نقطه

از این دو عملیات، در مجموع برای انجام ضرب نرده‌ای، یعنی R = a P استفاده می‌شود که به صورت جمع نقطه P به تعداد a مرتبه تعریف می‌شود.

R = 7P

R = P + (P + (P + (P + (P + (P + P)))))

فرآیند ضرب نرده‌ای را معمولاً می‌توان با استفاده از ترکیبی از عملیات جمع نقطه و دو برابر کردن نقطه ساده کرد. به عنوان مثال:

R = 7P

R = P + 6P

R = P + 2 (3P)

R = P + 2 (P + 2P)

در این‌جا، 7P به دو گام برای دو برابرسازی نقطه و دو گام برای جمع نقطه شکسته است.

میدان‌های محدود

در حوزه ECDSA، میدان محدود را می‌توان به عنوان مجموعه‌ای از پیش‌تعریف‌شده از اعداد مثبت دانست که تمام محاسبات باید در آن انجام شوند. هر عددی که در خارج از این محدوده قرار گیرد، به گونه‌ای «پیچیده می‌شود» تا در نهایت، در این محدوده واقع شود.

ساده‌ترین راه برای آن‌که بتوانید این مفهوم را درک کنید، محاسبه باقیمانده است که به صورت عملگر پیمانه (mod) نشان داده می‌شوند. به عنوان مثال، حاصل 9/7 برابر با 1 بوده و باقیمانده آن برابر با 2 است.

9 mod 7 = 2

در این مثال، پیمانه ما برابر با 7 است و تمامی عملیات mod که در این میدان انجام می‌شود، نتیجه‌ای در محدوده 0 تا 6 خواهد داشت.

در مجموع

در ECDSA از منحنی‌های سهموی در یک میدان محدود استفاده می‌شود. بدین ترتیب، معمولاً ظاهر عوض می‌شود، اما معادلات مربوط یا ویژگی‌های خاص آن تغییری نمی‌کند. همین معادله در بالا در میدان محدود با پیمانه 67 ترسیم شده است که چیزی شبیه به شکل زیر می‌شود:

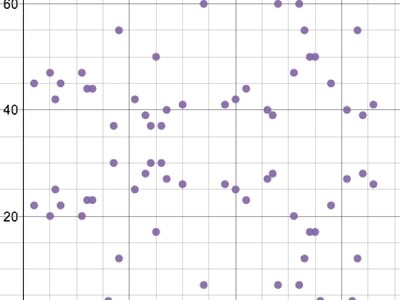
ریاضیات مربوط به بیت‌کوین

اکنون، مجموعه‌ای از نقاط داریم که در آن‌ها، مقادیر x و y به صورت اعداد صحیحی هستند که بین 0 و 66 قرار می‌گیرند. توجه داشته باشید که در این منحنی، همچنان تقارن افقی وجود دارد.

بنابراین، جمع و دو برابرسازی نقطه از نظر تصویری اندکی با هم فرق دارند. خطوطی که در این نمودار ترسیم می‌شوند، در جهت‌های افقی و عمودی و چیزی شبیه به بازی شبه‌ستاره‌ای به هم می‌پیچند و در عین حال، شیب خود را حفظ می‌کنند. بنابراین، جمع نقاط (2, 22) و (6, 25) چیزی شبیه به شکل زیر می‌شود:

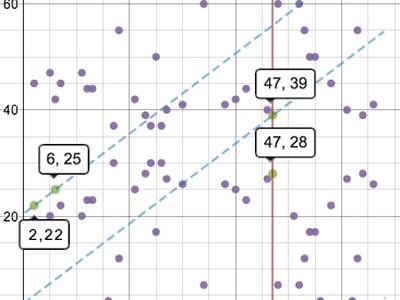
ریاضیات مربوط به بیت‌کوین

سومین نقطه تقاطع (47, 39) و نقطه بازتاب نیز (47, 28)  است.

برگردیم به ECDSA و بیت‌کوین

در پروتکل بیت‌کوین، مجموعه‌ای از پارامترها برای منحنی سهموی و نمایش میدان محدود آن انتخاب می‌شود که برای تمامی کاربران این پروتکل، یکی است. این پارامترها عبارتند از معادله مورد استفاده، پیمانه اصلی میدان و یک نقطه مبنا که بر روی منحنی قرار می‌گیرد. مرتبه نقطه مبنا که به صورت مستقل انتخاب نمی‌شود، اما تابعی از سایر پارامترهای دیگر است نیز بر روی نمودار به صورت تعداد دفعاتی نمایش داده می‌شود که نقطه به خودش اضافه می‌شود تا در نهایت، شیب به مقدار بینهایت برسد یا خط به صورت عمودی در آید. نقطه مبنا به گونه‌ای انتخاب می‌شود که مرتبه، به صورت یک عدد اولیه بزرگ باشد.

در پروتکل بیت‌کوین از اعداد بسیار بزرگ برای نقطه مبنا، پیمانه اصلی و مرتبه استفاده می‌شود. در واقع، در تمامی کاربردهای عملی ECDSA از مقادیر بزرگ استفاده می‌شود.

امنیت الگوریتم نیز بستگی به آن دارد که این مقادیر بزرگ باشند و بنابراین، امکان حمله جستجوی فراگیر یا مهندسی معکوس برای آن‌ها وجود نداشته باشد.

در مورد بیت‌کوین:

معادله منحنی سهموی: y2 = x3 + 7

پیمانه اصلی = 2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F

نقطه مبنا = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

مرتبه = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141

چه کسی این اعداد را انتخاب کرده است و به چه دلیل؟ تحقیقات زیادی در خصوص انتخاب پارامترهای مناسب انجام شده و مورد بررسی و مداقه قرار گرفته است. در نهایت، به نظر می‌رسد که اگر اعداد بزرگ باشند و به صورت تصادفی انتخاب شوند، دیگر روش درب پشتی (یا بک‌دور) برای ایجاد دوباره کلید خصوصی وجود نخواهد داشت. به طور خلاصه این‌که این کار با استفاده از چیزی به نام secp256k1 انجام می‌شود که در واقع، بخشی از راهکارهای منحنی سهموی بر روی میدان‌های محدود است که برای استفاده در رمزنگاری توصیه شده است.

کلیدهای خصوصی و کلیدهای عمومی

با مطالبی که بیان شد، اکنون وقت آن است که کلیدهای خصوصی و عمومی را بشناسیم و ببینیم که چه ارتباطی با یکدیگر دارند. مخلص کلام این است: در ECDSA، کلید خصوصی یک عدد است که به صورت غیر قابل پیش‌بینی بین عدد 1 تا عدد مرتبه، انتخاب می‌شود. کلید عمومی نیز از روی کلید خصوصی با استفاده از ضرب نرده‌ای این نقطه مبنا به تعداد دفعات برابر با کلید خصوصی به دست می‌آید. معادله به صورت زیر است:

نقطه مبنا * کلید خصوصی = کلید عمومی

این معادله نشان می‌دهد که بیشترین تعداد ممکن برای کلیدهای خصوصی (و بنابراین، آدرس‌های بیت‌کوین) برابر با عدد مرتبه است.

در یک میدان پیوسته می‌توانیم خط مماس را ترسیم کرده و کلید عمومی را بر روی نمودار نشان دهیم، اما معادلاتی هم وجود دارند که همین کار را در میدان‌های محدود انجام می‌دهند. جمع نقطه p + q برای یافتن r به صورت مؤلفه‌ای به شکل زیر تعریف می‌شود:

c = (qy – py) / (qx – px)

rx = c2 – px – qx

ry = c (px – rx) – py

و دو برابرسازی نقطه برای یافتن r نیز به صورت زیر است:

c = (3px2 + a) / 2py

rx = c2 – 2px

ry = c (px – rx) – py

در عمل برای محاسبه کلید عمومی، آن را به تعدادی از عملیات دو برابرسازی نقطه و جمع نقطه تقسیم می‌کنند که از نقطه مبنا آغاز می‌شود.

به مثالی با استفاده از اعداد کوچک استفاده می‌کنیم تا ببینیم که این کلیدها به چه شکلی ساخته شده و برای امضا و تأیید از آن‌ها استفاده می‌شود. پارامترهایی که از آن‌ها استفاده می‌کنیم، به شرح زیر است:

معادله: y2 = x3 + 7 (که در این مورد، a = 0 و b = 7)

پیمانه اصلی: 67

نقطه مبنا: (2, 22)

مرتبه: 79

کلید خصوصی: 2

ابتدا کلید عمومی را پیدا می‌کنیم. با توجه به این‌که ما ساده‌ترین کلید خصوصی با عدد برابر با 2 را انتخاب کرده‌ایم، صرفاً کافی است تا عملیات دو برابرسازی نقطه را از نقطه مبنا انجام دهیم. این محاسبه به شکل زیر است:

c = (3 * 22 + 0) / (2 * 22) mod 67

c = (3 * 4) / (44) mod 67

c = 12 / 44 mod 67

این‌جا باید صبر کنیم و کمی تردستی انجام دهیم: عمل تقسیم در یک میدان محدود باید به چه شکلی انجام شود تا نتیجه، همیشه به صورت یک عدد صحیح باشد؟ برای این کار باید عدد را در معکوس آن ضرب کنیم که در این‌جا، فضا به ما اجازه تعریف این کار را نمی‌دهد (در صورت لزوم، ما مرتب می‌گوییم این‌جا و این‌جا). در این‌ مورد، باید کمی و لحظه‌ای به ما اعتماد کنید:

44-1 = 32

با این فرض پیش می‌رویم:

c = 12 * 32 mod 67

c = 384 mod 67

c = 49

rx = (492 – 2 * 2) mod 67

rx = (2401 – 4) mod 67

rx = 2397 mod 67

rx = 52

ry = (49 * (2 – 52) – 22) mod 67

ry = (49 * (-50) – 22) mod 67

ry = (-2450 – 22) mod 67

ry = -2472 mod 67

ry = 7

بنابراین، یک کلید عمومی مربوط به نقطه (52, 7) می‌شود. همه این‌ها برای کلید خصوصی 2! جواب می‌دهد.

این عملیات، یعنی تبدیل کلید خصوصی به کلید عمومی، از نظر محاسباتی آسان‌تر از آن است که بخواهیم برگردیم و کلید خصوصی را از کلید عمومی استنباط کنیم. هر چند این کار از نظر تئوری امکان‌پذیر است، اما در عمل به خاطر تعداد پارامترهای زیادی که باید در رمزنگاری سهموی وارد شوند، از نظر محاسباتی شدنی نیست.

بنابراین، رسیدن به کلید عمومی از روی کلید خصوصی، از نظر طراحی یک سفر یک‌طرفه است.

کلید عمومی را هم همانند کلید خصوصی، معمولاً با یک رشته در مبنای شانزده یا هگزادسیمال نشان می‌دهند. اما صبر کنید؛ چگونه می‌توانیم از روی یک نقطه در یک صفحه که با دو عدد تعریف می‌شود به یک عدد مشخص برسیم؟ در یک کلید عمومی فشرده‌نشده، دو عدد 256-بیتی مختصات x و y را نشان می‌دهند که در یک رشته بلند به هم چسبیده‌اند. ما همچنین می‌توانیم از مزیت تقارن موجود در منحنی سهموی استفاده کرده و یک کلید عمومی فشرده را تولید کنیم. برای این کار باید مقدار x را نگه داریم و مشخص کنیم که نقطه در کدام نیمه از منحنی قرار گرفته است. با استفاده از همین اطلاعات می‌توانیم هر دو مختصات را به دست آوریم.

امضای داده با استفاده از کلید خصوصی

اکنون که یک جفت کلید خصوصی و کلید عمومی در اختیار داریم، می‌توانیم برخی از داده‌ها را امضا کنیم!

این داده‌ها می‌توانند هر مقدار طولی داشته باشند. معمولاً در گام اول، داده‌ها هش می‌شوند تا یک عدد به دست آید. این عدد همان تعداد بیت (256 بیت) برابر با عدد دسته منحنی را دارد. در این‌جا به منظور سادگی، گام هش را کنار گذاشته و فقط داده‌های ردیف z را امضا می‌کنیم. G را به عنوان نقطه مبنا، دسته و d را به عنوان کلید خصوصی در نظر می‌گیریم. روش امضا به صورت زیر است:

1. یک عدد صحیح k بین 1 و n – 1 انتخاب کنید.
2. با استفاده از ضرب نرده‌ای، نقطه (x, y) = k * G را محاسبه نمایید.
3. r = x mod n را پیدا کنید. در صورتی که r = 0 باشد، به گام 1 برگردید.
4. s = (z + r * d) / k mod n را محاسبه کنید. در صورتی که s = 0، به گام 1 برگردید.
5. امضا به صورت جفت (r, s) است.

برای باقیمانده، در گام 4، اگر اعداد حاصل به صورت کسری باشند (که معمولاً در دنیای واقعی، همیشه به همین صورت است)، صورت کسر باید در معکوس مخرج کسر ضرب شود. در گام 1، نکته مهم آن است که مقدار k نباید در امضاهای مختلف تکرار شود و نباید به صورتی هم باشد که اشخاص ثالث بتوانند آن را حدس بزنند. بدین معنا که k باید به صورت تصادفی بوده یا با استفاده از روش‌های قطعی که در اختیار اشخاص ثالث قرار نمی‌گیرد، تولید شود. در غیر این‌صورت می‌توان کلید خصوصی را از گام 4 به دست آورد، زیرا z، r و k همه و همه معلوم هستند. می‌توانید در خصوص یکی از سوء استفاده‌ها در این‌جا بیشتر بخوانید.

فرض کنید که داده‌ ما، عدد 17 است و قرار است تا روش بالا را برای آن پیاده کنیم. متغیرهای ما به صورت زیر است:

z = 17 (داده)

n = 79 (دسته)

G = (2, 22) (نقطه مبنا)

d = 2 (کلید خصوصی)

1. یک عدد تصادفی انتخاب کنید:

k = rand(1, n – 1)

k = rand(1, 79 – 1)

k = 3 (آیا این عدد واقعاً یک عدد تصادفی است؟ باشه، مچ ما را گرفتید، اما این عدد را فقط برای این انتخاب کرده‌ایم که مثال‌مان ساده‌تر شود!)

1. نقطه را محاسبه کنید. این کار به همان روشی انجام می‌شود که برای تعیین کلید عمومی به کار می‌رود، اما برای این‌که خلاصه‌تر کار کنیم، از حساب‌های جمع نقطه و دو برابرسازی نقطه صرف‌نظر می‌کنیم.

(x, y) = 3G

(x, y) = G + 2G

(x, y) = (2, 22) + (52, 7)

(x, y) = (62, 63)

x = 62

y = 63

1. r را پیدا کنید:

r = x mod n

r = 62 mod 79

r = 62

1. S را پیدا کنید:

s = (z + r * d) / k mod n

s = (17 + 62 * 2) / 3 mod 79

s = (17 + 124) / 3 mod 79

s = 141 / 3 mod 79

s = 47 mod 79

s = 47

توجه داشته باشید که در بالا ما می‌توانیم تقسیم بر 3 هم انجام دهیم، زیرا عدد حاصل به صورت یک عدد صحیح است. در دنیای واقعی می‌توانیم از معکوس k هم استفاده کنیم (در این‌جا هم همانند قبل، از بعضی جزئیات دشوار صرف‌نظر کرده و این‌ها را در جای دیگری انجام داده‌ایم):

s = (z + r * d) / k mod n

s = (17 + 62 * 2) / 3 mod 79

s = (17 + 124) / 3 mod 79

s = 141 / 3 mod 79

s = 141 * 3-1 mod 79

s = 141 * 53 mod 79

s = 7473 mod 79

s = 47

1. امضای ما به صورت جفت (r, ) = (62, 47) است.

همانند آن‌چه برای کلیدهای خصوصی و عمومی وجود دارد، در این‌جا هم امضا معمولاً به صورت یک رشته در مبنای شانزده نمایش داده می‌شود.

تأیید امضا به وسیله کلید عمومی در پروتکل بیت‌کوین

اکنون، مقداری داده و یک امضا برای این داده‌ها در اختیار داریم. شخص ثالثی که کلید عمومی ما را در اختیار داشته باشد، می‌تواند داده‌ها و امضای ما را به دست آورده و تأیید کند که او، خودش کسی است که ارسال می‌کند. ببینیم که چگونه عمل می‌شود.

اگر Q کلید خصوصی ما باشد و سایر متغیرها هم همانند قبل تعریف شود، گام‌های لازم برای تأیید امضا به صورت زیر خواهد بود:

1. تصدیق کنید که r و s بین 1 و n – 1 قرار دارند.
2. مقدار w = s-1 mod n را محاسبه کنید.
3. مقدار u = z * w mod n را محاسبه کنید.
4. مقدار v = r * w mod n را محاسبه کنید.
5. نقطه (x, y) = uG + vQ را به دست آورید.
6. تأیید نمایید که r = x mod n. اگر این‌طور نباشد، امضا نیز معتبر نخواهد بود.

چرا این گام‌ها جواب می‌دهند؟ در این‌جا اثبات را نمی‌آوریم، اما اگر دوست دارید، می‌توانید از این‌جا بخوانید. دستورالعمل را دنبال می‌کنیم و می‌بینیم که جواب می‌دهد. یک بار دیگر متغیرها را مرور می‌کنیم.

z = 17 (داده)

(r, s) = (62, 47) (امضا)

n = 79 (دسته)

G = (2, 22) (نقطه مبنا)

Q = (52, 7) (کلید عمومی)

1. تصدیق نمایید که r بین 1 و n – 1 قرار دارد. بررسی کنید و ببینید.

r: 1 <= 62 < 79

s: 1 <= 47 < 79

1. w را محاسبه کنید:

w = s-1 mod n

w = 47-1 mod 79

w = 37

1. u را محاسبه کنید:

u = zw mod n

u = 17 * 37 mod 79

u = 629 mod 79

u = 76

1. v را محاسبه کنید:

v = rw mod n

v = 62 * 37 mod 79

v = 2294 mod 79

v = 3

1. نقطه (x, y) را محاسبه کنید:

(x, y) = uG + vQ

دو برابرسازی و جمع نقطه را به صورت جداگانه در uG و vQ تقسیم می‌کنیم.

uG = 76G

uG = 2(38G)

uG = 2( 2(19G) )

uG = 2( 2(G + 18G) )

uG = 2( 2(G + 2(9G) ) )

uG = 2( 2(G + 2(G + 8G) ) )

uG = 2( 2(G + 2(G + 2(4G) ) ) )

uG = 2( 2(G + 2(G + 2( 2(2G) ) ) ) )

اندکی تأمل کنید تا ببینید که چگونه با استفاده از ترفند گروه‌بندی، 75 عملیات جمع متوالی را فقط به 6 عملیات دو برابرسازی نقطه و دو عملیات جمع نقطه کاهش می‌دهیم. وقتی که اعداد خیلی بزرگ می‌شوند، این عملیات واقعاً کار را راحت می‌کنند.

کار خود را از درون به بیرون آغاز می‌کنیم:

uG = 2( 2(G + 2(G + 2( 2( 2(2, 22) ) ) ) ) )

uG = 2( 2(G + 2(G + 2( 2(52, 7) ) ) ) )

uG = 2( 2(G + 2(G + 2(25, 17) ) ) )

uG = 2( 2(G + 2( (2, 22) + (21, 42) ) ) )

uG = 2( 2(G + 2(13, 44) ) )

uG = 2( 2( (2, 22) + (66, 26) ) )

uG = 2( 2(38, 26) )

uG = 2(27, 40)

uG = (62, 4)

و حال، برای vQ:

vQ = 3Q

vQ = Q + 2Q

vQ = Q + 2(52, 7)

vQ = (52, 7) + (25, 17)

vQ = (11, 20)

با این تفسیر داریم:

(x, y) = uG + vQ

(x, y) = (62, 4) + (11, 20)

(x, y) = (62, 63)

بدیهی است که گام 5، مجموع کار را به صورت کلی نشان می‌دهد. برای گام آخر،

1. تأیید نمایید که r = x mod n

r = x mod n

62 = 62 mod 79

62 = 62

بنابراین، امضای ما معتبر است!

نتیجه‌گیری

برای کسانی که همه معادلات را دیده‌اند و به این پایین نمی‌آیند، بگویم که چه چیزهایی یاد گرفته‌ایم.

ما در این‌جا اطلاعاتی را در خصوص پروتکل بیت‌کوین و رابطه ریاضی که بین کلیدهای عمومی و خصوصی وجود دارد، ارائه کرده‌ایم. ما به این نتیجه رسیده‌ایم که حتی در ساده‌ترین مثال‌ها هم اصول ریاضی مربوط به امضاها و تأییدها به سرعت پیچیده می‌شوند و وقتی که پارامترهای موجود به صورت اعداد 256 بیتی هستند، این پیچیدگی‌ها بیشتر هم می‌شود. همچنین، استفاده از روش‌های ریاضی به شکل هوشمندانه می‌تواند توابع «درب تله» (ترپ دور) ایجاد کند که برای حفظ عدم تقارن در اطلاعاتی ضروری هستند که مالکیت را برای یک بیت‌کوین تعریف می‌کنند. اخیراً هم به قوت سیستم اعتماد کرده‌ایم، مشروط بر این‌که بتوانیم به دقت از اطلاعات کلیدهای خصوصی محافظت کنیم.

به بیان دیگر، به همین دلیل است که گفته می‌شود پشتوانه پروتکل بیت‌کوین، یک سری از اصول ریاضی است.

اگر در بیت‌های پیچیده گیر کرده‌ بودید، امیدواریم که این اطلاعات توانسته باشد تا اعتماد به نفسی را در شما ایجاد کند تا گام بعدی را بردارید و خودتان، ریاضیات کار را انجام دهید (می‌توانید با استفاده از یک ماشین‌حساب ماژولار، ریاضیات مربوط به میدان محدود را بسیار ساده سازید). از طرفی، ما به این نتیجه رسیده‌ایم که اگر گام‌های امضا و تأیید داده‌ها را به صورت دستی انجام دهید، درک بهتری از رمزنگاری‌هایی پیدا می‌کنید که شکل منحصر بفردی از مالکیت را در بیت‌کوین به وجود می‌آورد.